Is a Lotto Ticket an Investment?

Have you ever wondered how much a lottery ticket is worth or how to value the potential winnings that it might provide? Because half of the income received from sales of jackpot games goes directly to the participating states, tickets are worth significantly less than their face value when prizes are normalized. But how much should you pay for the opportunity to win millions?
The value of a lottery ticket is not static but dependent on the potential payments to winners, which change as the jackpot is distributed or not. Although the probability of winning is set, the jackpots can increase over time, which changes the value of the investment opportunity. In most cases (when jackpots are normal), a lottery ticket is worth only a fraction of its cost. In periods when jackpots are supersized, the value of the opportunity may begin approaching the cost of the ticket. Although the increased demand for lottery tickets when jackpots are massive probably has more to do with greed, some of the demand can be explained by the fact that it makes better financial sense to purchase a lottery ticket when the cost approximates value.
Defining Expected Value
One way to determine the maximum amount you should pay for a lottery ticket, or any other investment opportunity, is by determining its expected value. The expected value of an investment opportunity is derived by determining each of the possible investment scenarios and then multiplying each scenario outcome by the probability of its occurrence. A probability-weighted average value of all possible outcomes provides the opportunity’s expected value.
Understanding the expected value of possible future results allows you to use mathematically sound reasoning when deciding to make an investment, pricing products and services, and prioritizing opportunities. Expected value provides investors not only with the maximum amount that they should commit to an investment but also with a way to compare across investments.
Calculating Expected Value
One way to determine the expected value is by using the mathematical equation. If X has n possible outcomes, the expected value is defined as
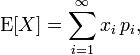
where p equals the probability of an event occurring and X equals the outcome of the respective event.
Although the formula might seem complicated, the actual derivation of expected value is quite easy. To demonstrate the calculation of expected value, let’s assume that there is a potential investment (Investment A) that has three distinct potential outcomes. The upside case, with a 25% probability of occurring, would yield $100,000; the base case, with a 50% probability of occurring, would yield $50,000; and the downside case, with a 25% probability of occurring, would yield $0. So, how much would you invest to gain an expected yield (expected value) of $50,000 as shown in this example? The amount to invest and the return required will always be personal choices based on the risks involved and other investment constraints that can be determined once the expected value or return is established.

Expected value of Investment A
Comparing Opportunities
Let’s also assume that there is another opportunity (Investment B) competing for the same scarce investment capital. This opportunity provides the following discrete scenarios: an upside scenario with a 30% probability of occurring that would yield $200,000, a base scenario with a 50% probability of occurring that would yield $40,000, and a downside scenario with a 20% probability of occurring that would result in a loss of $100,000. The expected value of the investment is calculated at $60,000.

Expected value of investment B
Expected value gives investors another way to compare opportunities. In our examples, and assuming that both investments require equal amounts of capital invested, Investment B has the higher expected value and thus should provide the highest potential return.
But unlike other metrics relating to return, expected value is not risk adjusted. Although Investment B has the higher potential return, it also has the highest potential risk. Investment B, with a mean of $47,000 and standard deviation of $150,000, is a much riskier endeavor than Investment A, which has a mean of $50,000 and a standard deviation of $50,000.
Valuing the Lottery
Using the expected value calculation and information easily obtained from the New York State Gaming Commission, it is possible to derive the expected value of a New York Lottery ticket. The probability and prize information shown in Figure A is taken from the $1 Take 5 instant game provided by the New York Lottery.
Because most instant games have set probabilities and prizes, their expected values will not change, regardless of how many people buy tickets. The expected value of the Take 5 game is calculated as $0.65, which means that, on average, players will lose $0.35 on each ticket. This $0.35, or 35%, also represents the average profit that the lottery earns on this particular game. Although the amount won each day will differ depending on what tickets are sold, over the long term, the lottery should only pay out about 65% of all the money that it has taken in from ticket sales.
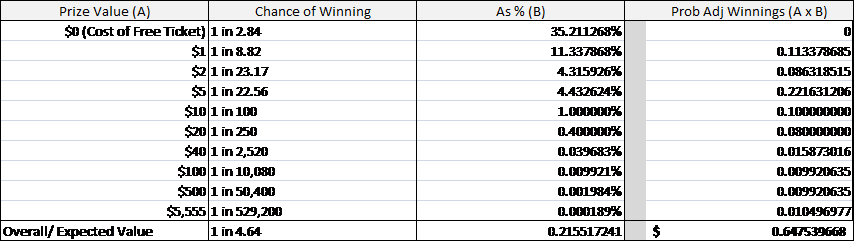
Take 5 — Prizes and Probabilities. Source: New York State Gaming Commission
So, what is a better value: the Powerball game, where you can win millions, or the $1 instant games, where you can win only thousands? Using the concept of expected value, we can compare the Take 5 instant game with the Powerball game and determine which provides a better opportunity for the amount invested in a ticket.
Determining the expected value for the Powerball jackpot requires the same methodology used to calculate the average gain or loss on the Take 5 game. Unlike the instant games, in which the expected value is set, the Powerball game’s expected value changes as the jackpot increases over time. In Powerball, a player must match six numbers (five plus the Powerball) with those numbers chosen during the lottery drawing. The probabilities are set and so are the prizes, with the exception of the grand prize, which can grow week to week if no one is successful in matching all six numbers. There are thus times when the Powerball game is a better value than Take 5, depending on the amount of the jackpot.
Figure B shows the prizes and probabilities for the popular $2 Powerball game:
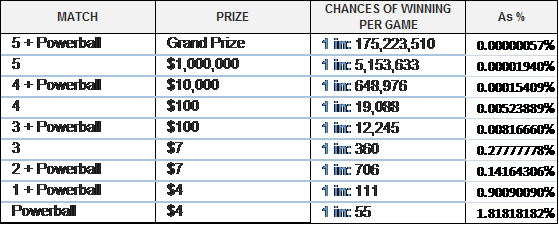
Powerball Game — Prizes & Probabilities. Source: Multi-state lotto association
To determine the value of a Powerball ticket, we must substitute the actual amount of the jackpot for a given week and then calculate the expected value by adding all the prizes adjusted for their probability of occurring. In a week when the jackpot is $50 million, the expected value of a ticket is only $0.65, meaning a player is expected to win, on average, $0.65 for each $2 ticket purchased. Put another way, when the jackpot is $50 million, a player will lose, on average, $1.35 for each ticket purchased ($0.65 – $2 = –$1.35). Now it may be obvious why so many people play the lottery when the jackpots get large — because players (investors) are receiving a better value for the money spent on the tickets. On the same game with a mega jackpot of $300 million, the expected value of the ticket equals $2.07, meaning that, on average, players will break even by winning approximately $2. During weeks when the jackpot is over $300 million, players will, on average, make a profit (i.e., win more than the cost of a ticket).
By comparing these two opportunities, we can see that when jackpots are small, the instant game is a much better deal than the jackpot games because of its lower cost and similar expected value. Although the maximum prizes that can be won in the instant games are much smaller, the probability of winning a prize is considerably higher; in the jackpot game, the opposite is true. When prizes in the jackpot games are supersized, it is these games that provide a better value by offering the chance to be ultra-rich and an expected value where players win, on average, as much as their tickets cost.
If you liked this post, don’t forget to subscribe to Inside Investing via Email or RSS.



Your EV calculations assume that there will only be one winner of the lottery. Often when there is a huge jackpot, there will be multiple winners splitting the jackpot, which reduces EV. The math behind this is nontrivial. You’re also ignoring tax issues and the fact that the jackpot is paid as an annuity whose present value is considerably less than the headline amount.