Editor’s Note: We find that many investors are confused when financial professionals talk about what interest rates will be in three years. This article explains something that is intuitive if considered properly: we can apply judgment to the present and learn something about what’s expected in the future.

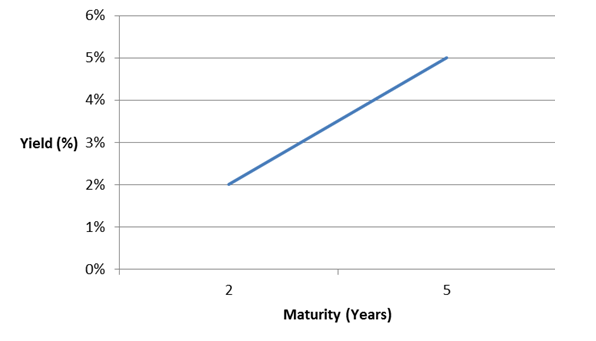
Assume we must choose between two investments. The first matures in two years and has a yield of 2%. The other matures in five years and has a yield of 5%.

This scenario creates a yield curve, like this:

All right, fine — technically, it’s a yield line.

In any case, this is also referred to as a “term structure of interest rates” and in this case, it is upward sloping. In plain English, rates in the distant future (five years) are higher than rates in the near future (two years).

First, Let’s Compare the Two Investments

If we choose to invest for two years, what will happen?

Assuming the investment compounds annually at the end of the first year, or “compounding period,” we would have $102. Mathematically, it would look like this:

$100 × 1.02 = $102.

That seems simple enough. Continuing on, at the end of the second year, we would have

$102 × 1.02 = $104.04.

If we wrote out the whole process as one formula, it would look like this:

$100 × (1.02) × (1.02) = $104.04.

And because there are two compounding periods, or two years, we multiply by 1.02 twice. We can simplify this formula by rewriting “1.02 × 1.02” as “1.02²” or 1.02 squared or 1.02 raised to the second power. Take your pick! So, our new formula now looks like this:

$100 × (1.02)² = $104.04.

Looking at Five Years

The five-year investment would look like this (and remember, it earns 5% a year):

$100 × (1.05) × (1.05) × (1.05) × (1.05) × (1.05) = $127.63

or

$100 × (1.05)⁵ = $127.63.

How Does This Imply Forward Rates?

We’re almost there. Before we get to the mechanics, Let’s take a hard look at each piece of that last formula:

• The “$100” is our initial investment or outlay. It’s the money we have today to invest. Let’s call that the present value (PV).
• The “.05” represents the interest rate (i) we are receiving, which is added to 1, or 100% of our initial investment, every compounding period.
• The “5” is our exponent and represents the number of compounding periods. It can be referred to as t (time) or n (number of periods).
• The “127.63” is the amount of money we end up with after five years. That’s the amount we will have in the future, or future value (FV).

We can rewrite our equation so that it will work for any number of periods or rates:

PV × (1 + i)^t = FV.

Figuring out the Future

Do you remember our investment choices? We could invest for two years or five years. Deciding which one to invest in is complicated as well as subjective in many cases, but not everything is subjective.

If we invest for two years, we get $104.04. If we invest for five years, we get $127.63. Because of something called “arbitrage pricing theory” investors must be indifferent as to whether they invest for two years or five years.

This means that at the end of the day (in five years) both investments have to end up with the same value: $127.63.

So, according to this theory, there must be some rate that will exist at the end of two years that will turn my $104.04 into $127.63 in the remaining three years.

In fact, that future or forward rate is already implied by the term structure that exists today. (Look at you, talking like a bond king!)

So, again, two years from now there will have to be some rate at which I can invest my $104.04 for the remaining three years to end up with $127.63. How might we figure that out?

We can use our formula. It seems as if we have all the necessary inputs except for the three-year rate two years from now. (By the way, that was the confusing part.)

So, our formula now looks like this:

$104.04 × (1 + i)³ = $127.63.

Now it’s just a simple matter of solving for i. (OK, it’s simple if you recently aced a high school algebra class!)

Rearranging the formula, we get

(1 + i)³ = $127.63/$104.04.

Simplifying by taking the nth root (in this case, the cube root) of both sides:

(1 + i) = ($127.63/$104.04)^1/3.

Subtracting 1 from both sides, we get

i = [($127.63/$104.04)^^1/3] – 1.

Thus, i = 0.070489, which, in decimal form, represents 7.05% (rounding up).

In other words, you would need to invest your $104.04 for the remaining three years at roughly 7.05% to end up with the same amount as the investor who initially chose to invest for five years.

That’s what an implied forward rate is. It is the rate that must be implied by the current term structure of interest rates for two investors to be indifferent to which maturity they pick.

Conceptually (and this is where the fun comes in), the investor who chooses to tie up his money for five years must believe that in two years’ time, rates on three-year pieces of paper will be lower than 7.05% and then invest accordingly. To a certain degree, choosing your maturity is, in and of itself, a bet on which way rates will go in the future.

I think another point of confusion arises from the fact that the concept of implied forward rate does not necessarily mean that two years from now three-year investments will be yielding 7.05%; it just means that, mathematically, that’s what is being implied today by the rates themselves. Those rates can and will change.

Naturally, we could do the same exercise for any two maturities. If we look at both a three-year and a seven-year combination, the implication is that three years from now, a four-year investment would make me whole—that is, equal to the investor who chose the seven-year investment.

If you liked this post, don’t forget to subscribe to Inside Investing via Email or RSS.