Sculpting Investment Portfolios: Maximum Drawdown and Optimal Portfolio Strategy

The fundamental aim of any portfolio construction methodology is to deliver optimal risk-adjusted performance.
While “risk” can be defined in a number of ways, maximum drawdown is probably one of the clearest ways to measure an investor’s risk appetite and thus is an important factor to consider when building portfolios. This post discusses the different ways in which maximum drawdown can be used as a risk factor to construct optimal portfolios.
Financial Markets and Fractals
Most portfolio/risk management models make assumptions about asset returns that are not entirely appropriate in the real world. The normality of the return distribution and the statistically “independent” nature of returns are two such key assumptions. Based on a normal distribution, the S&P 500 Index should have had only 1.3 months of –15% or worse returns over the past 85 years.
However, the S&P 500 has had about 10 such months in the past 85 years. Hence, assuming a normal distribution or independence of returns can lead to a severe underestimation of “real world” risk. Statistical independence of returns means yesterday’s return has no influence on today’s, and similarly, today’s price has no influence on the change between current price and tomorrow’s price. This basically means that predicting future market returns is impossible. However, positive serial correlation does exist, which leads to temporary bouts of up or down rallies depending on the sentiment prevailing in the market. As a result, risk measures that depend on the above assumptions end up masking and underpricing true risk.
According to Mandelbrot (2008), a financial time series can be better modeled using fractal geometry. A fractal is a geometric shape that can be separated into parts, each of which is a reduced scale version of the whole. Examples of fractal patterns include coastlines, cauliflowers, and distributions of galaxies. Mandelbrot claims that fractals and multi-fractals generate a more realistic picture of market risks and can be used to better stress-test portfolios.
Drawdowns and Maximum Drawdown
Maximum drawdown (MDD) is the accumulated loss of buying an investment at its highest local maximum price and selling it at its lowest local minimum price. The term “local” refers to the time horizon over which the investment is analyzed or transacted. Drawdown, in contrast, refers to the decline in value from the previous local maximum to a subsequent trough. An investment may have many drawdowns over a period of time but has only one MDD.
Figures 1 and 2 exhibit the drawdowns and MDD for the MSCI Emerging Markets Index based on monthly total return data from September 2001 to September 2011.
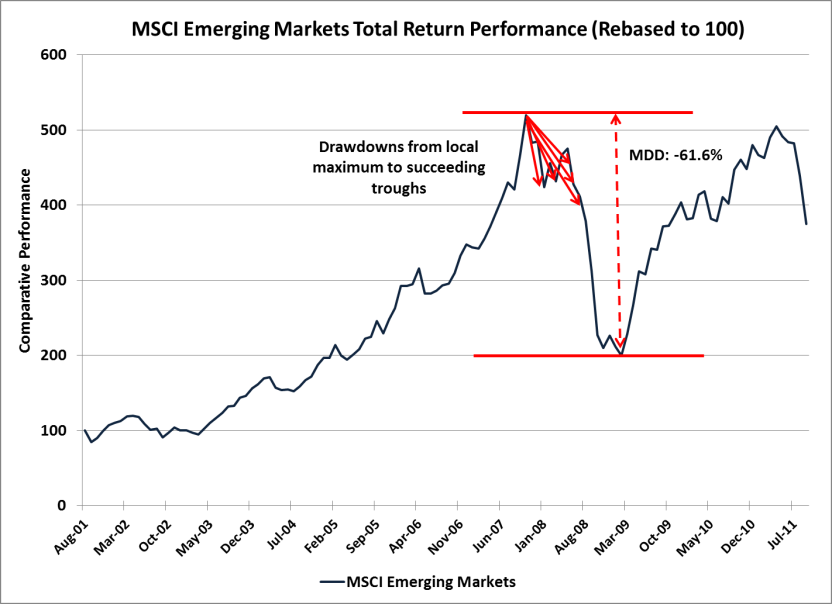
Figure 1 | Data Source: Bloomberg
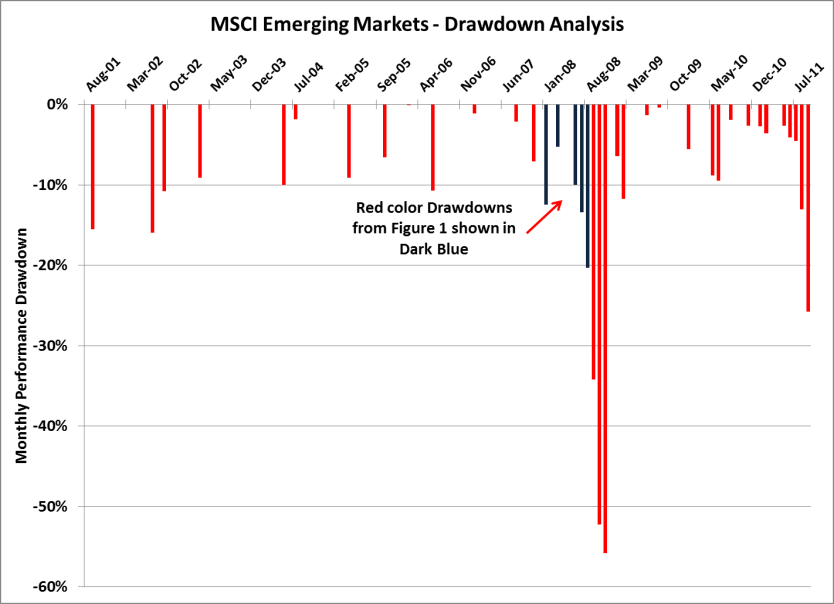
Figure 2 | Data Source: Bloomberg
Apart from the time horizon under consideration, the magnitude of drawdowns also depends on the frequency of measurement. For instance, over a one-year period, the drawdown of an investment measured in monthly returns may be significantly lower than the drawdowns measured on a daily basis. This is because there are a greater number of data points when using daily data compared with using monthly data.
Significance of Maximum Drawdown
Clients, both retail and institutional, place a lot of importance on MDD. Even though the performance of a portfolio is to be measured against its long-term objectives, short-term performance matters, especially when there is a market sell-off.
Under such circumstances, the value of active portfolio management is brought to the fore by comparing the MDD of the portfolio with the markets’ MDD. Strong drawdowns may force traders to temporarily stop trading and may even lead to a re-evaluation of their trading strategy. In the case of leverage, drawdowns have a much larger effect on portfolio performance.
The two most important moments of a distribution are the mean and standard deviation of the distribution. Most investors and portfolio managers focus on these two parameters to build risk-optimal portfolios. Volatility masks true portfolio risk when skewness and kurtosis are not taken into account or when the return distribution exhibits strong positive serial correlation. In such cases, MDD is a handy measure to evaluate “expected worst case” risk.
A very interesting property of MDD is that it’s not sensitive to additional data points that do not violate the local maximum or minimum values. Normally in a financial time series, if any number of relatively stable returns is added, all variance-based measures (such as volatility, downside deviation, or semi-variance) are affected. However, the MDD of the series is not affected, and it serves to remind investors and managers of the worst possible outcome even during relatively calm periods.
Calmar Ratio
The Calmar ratio is frequently used as a risk measure that takes MDD into account. The Calmar ratio is simply defined as the compounded annualized growth rate divided by the MDD over the same period. However, unlike the Sharpe ratio, the Calmar ratio cannot be scaled for different time periods. Hence, in order to use the Calmar ratio to compare portfolios, the analysis has to be carried out over the exact same time periods.
Magdon-Ismail and Atiya presented analytical results in 2004 that related the expected MDD to the mean and volatility of returns. They also introduced a measure called the “normalized Calmar ratio,” which can be used to quote and compare Calmar ratios of portfolios over different time frames.
Portfolio Optimization with Drawdown Constraints
During periods of stress, diversification through passive asset allocation or “balanced portfolios” (e.g., 60% stock/40% bond portfolios) is not very helpful because asset correlations move up quite rapidly and dramatically. Optimization tools that use variance as a risk measure do not perform well in terms of drawdown because variance is a path-independent statistical attribute. Hence, specific drawdown-based constraints need to be used in an optimization process to control for MDD explicitly.
Alexi Chekhlov and some other researchers proposed a new measure called CDaR (conditional drawdown at risk), which uses drawdown to define the loss function.
The function works like this: For some tolerance value β, the CDaR is defined as the mean of the worst (1 – β) × 100% of drawdowns.
So for instance, 0.90 CDaR is the average of the worst 10% drawdowns over the considered time interval. The CDaR takes into account both the size and duration of the drawdowns, with MDD and average drawdown as its limiting cases. For portfolio optimization, using a CDaR is better than using just a single MDD because the statistical averaging within the (1 – β) × 100% of drawdowns has more predictive power than just a single observation of maximal loss.
Conclusion
Even though MDD as a risk measure has some desirable properties, it is to be used with caution. Focusing on MDD as a key criterion in decision making indicates extreme risk aversion and is relevant if and only if one expects to buy and sell at the worst possible time.
However, MDD starts to get more valuable when used along with the drawdown distribution and such other analytics as the Calmar ratio and up/down capture ratio. It is also possible to construct portfolios aimed at protecting against certain future MDDs by incorporating MDD-related constraints in the optimization process.
If you liked this post, don’t forget to subscribe to Inside Investing via Email or RSS.
Please note that the content of this site should not be construed as investment advice, nor do the opinions expressed necessarily reflect the views of CFA Institute.
Photo credit: iStockphoto/ShannonToth


